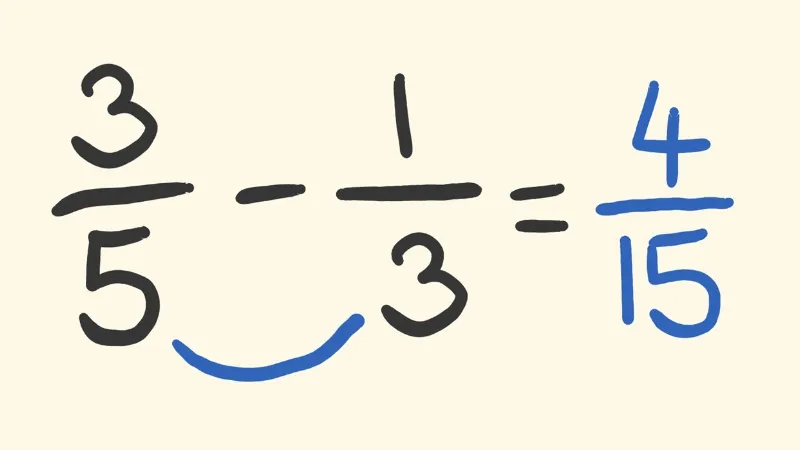It may initially appear difficult to subtract fractions, especially those with different denominators. It’s fairly simple, though, once you understand a few fundamental principles.
We must first comprehend how a fraction is made up. The numerator and the denominator are the two components in this equation, and they are divided by a dividing line.
The denominator is the bottom figure. This demonstrates the number of equally sized pieces that one whole has been divided into. The top figure, known as the numerator, indicates the number of components that make up the whole.
We must make sure that the whole we are dealing with in both cases is divided into the same number of equal parts, i.e., two, in order to successfully subtract one fraction from another. that the denominators are the same.
When subtracting fractions with various denominators, there are a few quick techniques you can use. Since you must use the conventional approach when asked to demonstrate your workings in any official exam, we’ll go over it in more detail below.
The same guidelines apply whether you’re working with proper fractions (where the numerator is less than the denominator) or improper fractions (where the numerator is greater than the denominator).
Continue reading.
Table of Contents
Introduction to Fractions
A fraction is a number that reflects the components of the whole. The numerator and the denominator are the two components that make up a fraction. The denominator is the lower portion of the fraction while the numerator is the upper portion. A fraction is, for instance, 7/9. In this case, the numerator is 7 and the denominator is 9. Different kinds of fractions can be categorized according to the numerator and the denominator. They are:
Proper Fraction: A proper fraction has a numerator that is less than its denominator. For instance, 35, 25, etc.
Improper Fraction: In improper fractions, the numerator is greater than the denominator. Example, 9/7, 11/9, etc.
Mixed Fraction: Combining the correct fraction with a whole number creates the mixed fraction. Example 2: 4 2 3; 5; etc.
Unit Fraction: In unit fraction, the numerator should be equal to 1. 13, ¼, 15, etc. are a few examples.
Equivalent Fractions: The fractions that have the same value as one another are called equivalent fractions. The equivalent fractions can be obtained by multiplying or dividing the numerator and denominator by the same number. Example, 2/4, 4/8, 8/16, etc
Like Fractions: Similar denominators are referred to as like fractions when referring to fractions. Example: 3/2, 5/2, 7/2, etc
Unlike Fractions: Like fractions are those that have two different denominators. Examples include 2/7, 2/9, 3/11, and so forth.
What is Meant by Subtracting Fractions?
In mathematics, the process of removing two fractional values is known as subtracting fractions. We have learned to subtract the whole numbers. For instance, 2 is obtained when 3 is subtracted from 5. (i.e. 5-3 = 2). In a similar manner, we can subtract operations on fractions. Subtracting Fractions include:
- Subtracting Fractions with Like Denominators
- Subtracting Fractions with Unlike Denominators
- Subtracting Mixed Fractions
- Subtracting Fractions with Whole Numbers
Let’s now go over each of these fractions that can be subtracted in detail with examples.
How to Subtract Fractions With Different Denominators?
Find the Least Common Denominator
The lowest common multiple between the two denominators you’re working with is the least common denominator, or LCD.
As an illustration, since we are instructed to subtract 2/3 from 2/6 and we are aware that 6 is a multiple of 3, 6 serves as our LCD.
Find the Equivalent Fraction
Once you’ve located the LCD, you must maintain the same value for all of your fractions. In order to change the numerator, you must also change the denominator.
We are dividing 3 by 2 in the aforementioned example to obtain a denominator of 6. Additionally, we must multiply 2 (the numerator) by 2 to maintain an equal value fraction. This gives us a fraction that is equivalent to 4/6.
For the second fraction, repeat this procedure. Since the denominator in our example is already 6 there is no need to make any changes.
A new equation of the form 4/6 – 2/6 exists now.
Subtract the New Numerators
The next step is simple: just subtract the numerators from your new equation. In this case, 4 – 2 = 2.
Put the resultant number over the common denominator. This gives us 2/6.
Simplify the Answer If Necessary
The final step is, if at all possible, to simplify the fraction. To do this, you’ll need to find the highest common factor shared by both parts of the fraction and divide them by it.
The most prevalent common factor for 2/6 is 2. Since 2 divided by 2 equals 1 and 6 divided by 2 equals 3, our fraction is 1/3.
2/3 – 2/6 = 1/3

Frequently Asked Questions
What is Meant by Subtracting Fractions?
In mathematics, subtracting fractions refers to the operation of removing fractions with comparable or dissimilar denominators.
How Do You Subtract the Fractions With the Same Denominators?
When the denominators of two fractions are the same, you can simply the resulting fraction by subtracting the numerators directly.
How Do You Subtract the Fractions With Different Denominators?
While subtracting fractions with different denominator, follow the steps given below:
Get the denominator’s LCM first.
Step 2: By multiplying the numerator and denominator by the same number, convert the denominators to the LCM Value.
Step 3: Subtract the numerator after the denominator has reached equality.
Step 4: Simplify the resulting fraction, if necessary.
Can We Subtract Fractions With Whole Numbers?
Fractions can be subtracted from whole numbers, yes. Divide the whole number by 1, then perform the subtraction operation to convert the whole number into fractions.
Summary: How to Subtract Fractions With Different Denominators?
We learned about the subtraction of fractions with dissimilar denominators in this article.
We must first comprehend how a fraction is made up. The numerator and the denominator are the two components in this equation, and they are divided by a dividing line.
The denominator is the bottom figure. This demonstrates the number of equally sized pieces that one whole has been divided into. The top figure, known as the numerator, indicates the number of components that make up the whole.
We must make sure that the whole we are dealing with in both cases is divided into the same number of equal parts, i.e., two, in order to successfully subtract one fraction from another. that the denominators are the same.
When subtracting fractions with various denominators, there are a few quick techniques you can use. Since you must use the conventional approach when asked to demonstrate your workings in any official exam, we’ll go over it in more detail below.
The same guidelines apply whether you’re working with proper fractions (where the numerator is less than the denominator) or improper fractions (where the numerator is greater than the denominator).
Read about